If someone has already discovered this technique and posted a reference to it here, I apologize, and will remove the post if it contributes nothing further. I've done searches and haven't found anything, but I may have missed something.
Anyway, here goes. On the RawDigger site, there's
a technique for computing Unity Gain ISO. It is basically a search over several exposures made with the camera ISO setting at different places for the ISO setting that, with a flat, relatively bright (but not saturated) compact target rectangle, produces a standard deviation in the (pick a channel) raw values that's the square root of the mean raw value in that channel.
I thought there ought to be a way to do the same thing without a search. I applied some algebra to the problem, and came up with the following algorithm: Set your camera to some middling ISO; call that value ISOtest. Point your camera at a featureless target. Defocus a bit to make sure you don't have any detail. Expose so that the target is about Zone VI, or a count of about 4000 for a 14-bit ADC. If you have a 12-bit ADC in your camera, try for a count of 1000. Bring the resultant image into RawDigger, select a 200x200 pixel area, and read the mean and standard deviation for each color plane. For each plane, call the mean Sadc and the standard deviation Nadc. The unity gain ISO is ISOtest*Sacd/(Nadc^2). Average all three color channels for the Unity Gain ISO of the camera.
I tried the algorithm out on a Nikon D4 over a range of ISOtest values, making 16 exposures for each ISOtest value and plotting the mean Unity Gain ISOs, the mean plus two standard deviations, and the mean minus two standard deviations.
The result looks like this:
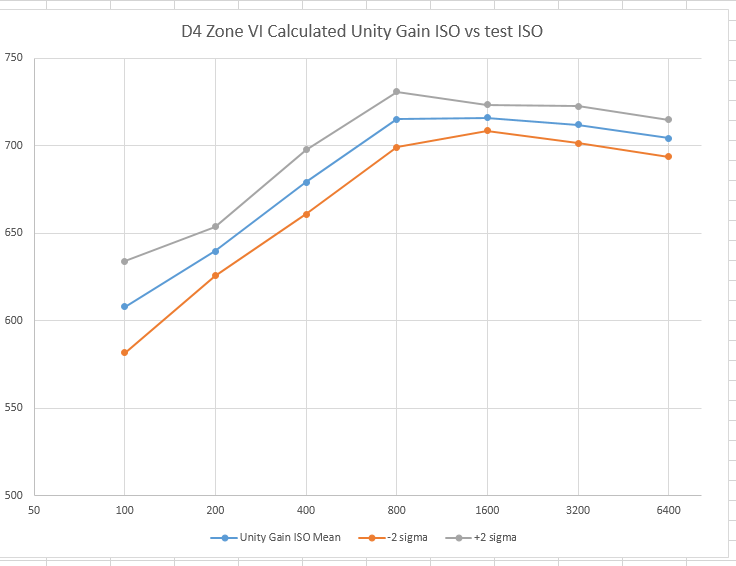
All of the Unity Gain ISOs are within about a third of a stop, so the accuracy is probably good enough to make this a useful measurement; I don't know why I'd want to know the Unity Gain ISO to greater accuracy than that. There is some systematic variation. Some of it may be due to the fact that, for the measurements at ISO 100, 200, and 400, the camera is below the Unity Gain ISO and the statistics of the image my be affected enough to skew the results. I'll be doing some simulation to see if that's a reasonable explanation.
I've done tests at other exposure levels (mean raw values) and the results are only weakly dependent on exposure. I've done similar tests on the following cameras: Nikon D800E, Leica M9, Sony NEX-7, and Sony RX-1, and, with the marginal exception of the Leica, all the results for each camera model cluster within a third of a stop of each other.
The math I used to derive the above equation and the Nikon D4 results are
here. The results for the other cameras are
here.
I welcome discussion on what might be the source of the systematic variations, which indicate that the simple model I used is incomplete. In the case of the Sony cameras, the raw files are compressed in a way that reduces the resolution in the lighter values. That might be a possible source. I think the value of understanding the systematic variation is to better understand the internal makeup of the cameras, since the test appears to be sufficiently accurate even with this variation.
jim