Having got out my college physics book, I will now prove that focal length does not affect resolution loss due to diffraction. *drum roll*
Now, we know that diffraction creates these 'Airy disks' which look like bulls-eyes - a central dot surrounded by concentric rings. The smaller the aperture, the bigger this central dot becomes - this is as described in
http://www.cambridgeincolour.com/tutorials...photography.htm, to wit:
When the diameter of the airy disk's central peak becomes large relative to the pixel size in the camera (or maximum tolerable circle of confusion), it begins to have a visual impact on the image. Alternatively, if two airy disks become any closer than half their width they are also no longer resolvable (Rayleigh criterion).
Some images may help, hopefully he won't mind me linking them here:
Airy disk in 2D

Airy disk in 3D
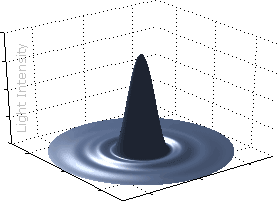
In order to figure out the maximum resolution of a lens, we figure out the angular separation of two points which are barely resolved - which for the purposes of this exercise will be two points whose central dots are just touching edge-to-edge - this will be the same as the angular size of either central peak.
The equation to figure this out is:
sinθ = 1.22(
λ/D)
Where
θ is the angular separation,
λ is the wavelength of light (considered a constant in this exercise, and set at 500nm) and
D is the aperture diameter.
For simplicity's sake, we'll make
sinθ just plain old
θ, as
θ is so small in any real world scenario to make the difference negligible. That gives us:
θ = 1.22(
λ/D)
Now, the experiment: We take two lenses, of 50mm and 100mm focal lengths, and set their apertures to f/2. Take a picture of an object 10 meters away with the 100mm lens, and one of an object 5 meters away with the 50mm lens. We'll take the wavelength of light to be 500nm as a constant.
We do this because for this experiment to be valid, the size of the image on the negative/sensor must be the same for both lenses. Since a 100mm lens gives 2x the magnification of a 50mm lens, we stand back twice the distance with the 100mm lens.
For the 50mm lens,
D, the aperture diameter is
50/2 = 25mm.
This gives us:
θ = 1.22(500x10⁻⁹/25x10⁻³)
so...
θ = 2.44x10⁻⁵ rad
For the 100mm lens,
D, the aperture diameter is
100/2 = 50mm.
This gives us:
θ = 1.22(500x10⁻⁹/50x10⁻³)
so...
θ = 1.22x10⁻⁵ rad
So, what does that tell us? It tells us that the Airy disk of the 100mm lens is half the angular size of that of the 50mm lens. This is critical to understanding why focal length doesn't matter in terms of diffraction. Longer lenses produce a narrower 'beam' of diffracted light - remember, the number above is in 'rad', so it's an angle, not a distance.
Even though the diffracted light has to travel further to reach the film/sensor in the 100mm lens than the 50mm lens, it's spreading out much more slowly. By the time it reaches the film/sensor it will produce a spot of light exactly as large as the 50mm lens does.
Now to prove this concretely, we want to measure what that means in terms of resolution. To do this, we want to measure the minimum distance between two points on an object that can be resolved with both lenses at the distances and aperture given.
From basic optics:
y/s = y'/s'Where
y is the separation of the points on the object,
y' is the separation of the corresponding points on the film/sensor,
s is the distance from lens to object and
s' is the distance from lens to film/sensor.
Thus the angular separations of the object points and the corresponding image points are both equal to
θ, so we get:
y/s = θand
y'/s' = θBecause
s is greater than the focal length of the lens, the image distance
s' is approximately equal to the focal length.
For the 50mm lens,
s = 5m,
s' = 50mm and
θ = 2.44x10⁻⁵ rad:
y/5m = 2.44x10⁻⁵
so...
y = 1.22x10⁻⁴m = 0.122mm
and
y'/50mm = 2.44x10⁻⁵
so...
y' = 1.22x10⁻³mm = 0.00122mm
For the 100mm lens,
s = 10m,
s' = 100mm and
θ = 1.22x10⁻⁵ rad:
y/10m = 1.22x10⁻⁵
so...
y = 1.22x10⁻⁴m = 0.122mm
and
y'/100mm = 1.22x10⁻⁵
so...
y' = 1.2x10⁻³mm = 0.00122mm
Phew! So, where does that leave us? Both lenses can resolve a minimum distance of .122mm on an object, which translates to a minimum resolvable dot on the film/sensor of .00122mm at those distances and an aperture of f/2. If we change the aperture, we will get different numbers, but the important thing is that they are the same for both lenses - so we've just proved that for the same image size and the same aperture, but different focal lengths, resolution is identical.
Again, the reason for this is that the longer lens produces a narrower cone of diffraction, so even though the light has to travel further to get to the film/sensor, it ends up producing the same size spot of light in both cases.
Thus, focal length does not contribute to resolution loss from diffraction.
Cheers,
Peter