Hi all, I am doing some tests about local/global contrast algorithms and need a simple equation to define an arbitrary S-shaped contrast curve. It's simple if the turning point is assumed to be (0.5, 0.5), but couldn't find a straight equation if the turning point has to be arbitrarily set.
These are the typical contrast curves I achieved for turning point in the middle (0.5, 0.5):
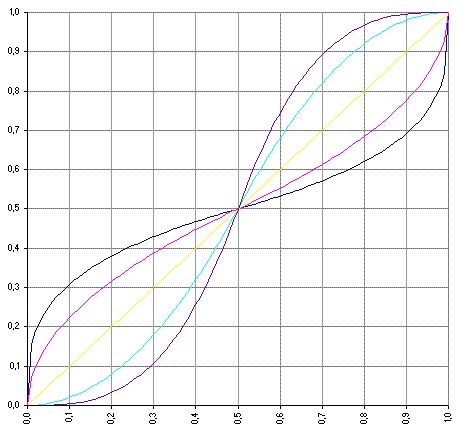
And the simple equations follow this rule:
y = x^2*2 for x<=0.5
y = 1-(1-x)^2*2 for x>0.5
I would like to be able to allocate the turning point to any (x,y) position and still have a smooth S-shaped curve where the slope is continuous on both sides of the turning point. If would like to keep the equation as simple and straightforward as possible, avoiding the use of splines or any other more complex math.
Your curve
is a spline -- a piecewise polynomial curve with conditions of continuity of the curve and its first derivative at the segment boundaries.
Just for fun, take the first curve and scale it:
y = a*(x/a)^2
This is a curve which reaches y=a at x=a, and has slope 2 at that point; and slope zero at x=0. If we take your second curve and scale it by (1-a):
(1-y) = (1-a)*((1-x)/(1-a))^2
this is a curve which reaches 1-y=1-a at 1-x=1-a, or in other words y=a at x=a; it has slope 2 at that point; and slope zero at x=1, where also y=1. So we have a sigmoidal curve with slope zero at x=0 and x=1, and slope 2 at x=a where the curve crosses the straight line x=y.
Now we can add a control parameter: Take the above curve, call it f(x); now form the curve
y = (1-s)*x + s*f(x)
This is a curve that has slope (1-s) at x=0 and x=1; and slope (1-s)+2*s=1+s at x=a. Thus by dialing s between 0 and 1, the slope at the neutral point x=a (where y=a of course) is dialed between 1 and 2; the contrast is gradually increased, and the curve is monotonic. For contrast decrease, you can either allow s to be negative, or if you want the effect to be symmetric about s=0, you want to interchange the roles of y and x in this regime.