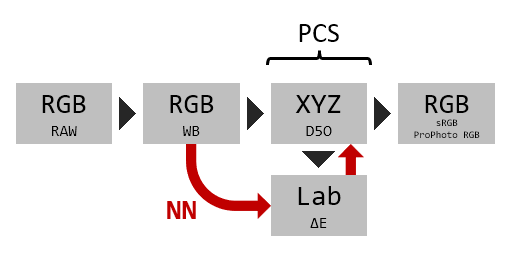
I have loop nested several NN's to save training time. I don't like too much this way of doing things (just try a gridsearch combination of hyperparameters and see which one performs best, without knowing why), but here it is. The format is: XYZ/Lab output, NN hidden layers, hidden layers activation function, output activation function:
MLP_XYZ_()_relu_identity : ΔE_max = 29.5782 , ΔE_mean = 3.4459 , ΔE_median = 2.4032
MLP_Lab_()_relu_identity : ΔE_max = 82.2025 , ΔE_mean = 28.3684 , ΔE_median = 21.2329
MLP_XYZ_()_logistic_identity : ΔE_max = 29.5782 , ΔE_mean = 3.4459 , ΔE_median = 2.4032
MLP_Lab_()_logistic_identity : ΔE_max = 82.2578 , ΔE_mean = 28.3821 , ΔE_median = 21.2219
MLP_XYZ_(3, 3)_relu_identity : ΔE_max = 108.3430 , ΔE_mean = 41.8331 , ΔE_median = 37.0897
MLP_Lab_(3, 3)_relu_identity : ΔE_max = 112.5269 , ΔE_mean = 42.6017 , ΔE_median = 39.5577
MLP_XYZ_(3, 3)_logistic_identity : ΔE_max = 23.9131 , ΔE_mean = 4.5645 , ΔE_median = 2.9977
MLP_Lab_(3, 3)_logistic_identity : ΔE_max = 77.6024 , ΔE_mean = 25.7275 , ΔE_median = 20.5809
MLP_XYZ_(50, 50)_relu_identity : ΔE_max = 13.7616 , ΔE_mean = 2.1762 , ΔE_median = 1.6024
MLP_Lab_(50, 50)_relu_identity : ΔE_max = 12.9015 , ΔE_mean = 3.6170 , ΔE_median = 3.1430
MLP_XYZ_(50, 50)_logistic_identity : ΔE_max = 22.5918 , ΔE_mean = 4.0708 , ΔE_median = 2.6891
MLP_Lab_(50, 50)_logistic_identity : ΔE_max = 6.0237 , ΔE_mean = 0.9943 , ΔE_median = 0.6923MLP_XYZ_(200, 200)_relu_identity : ΔE_max = 7.0373 , ΔE_mean = 1.0364 , ΔE_median = 0.6827
MLP_Lab_(200, 200)_relu_identity : ΔE_max = 7.4150 , ΔE_mean = 1.1333 , ΔE_median = 0.8822
MLP_XYZ_(200, 200)_logistic_identity : ΔE_max = 14.8826 , ΔE_mean = 2.7814 , ΔE_median = 1.8480
MLP_Lab_(200, 200)_logistic_identity : ΔE_max = 5.6598 , ΔE_mean = 0.8287 , ΔE_median = 0.4912MLP_XYZ_(200, 200, 200)_relu_identity : ΔE_max = 6.3270 , ΔE_mean = 1.2530 , ΔE_median = 0.7609
MLP_Lab_(200, 200, 200)_relu_identity : ΔE_max = 7.3421 , ΔE_mean = 0.9603 , ΔE_median = 0.7042
MLP_XYZ_(200, 200, 200)_logistic_identity : ΔE_max = 14.4747 , ΔE_mean = 2.7297 , ΔE_median = 1.9047
MLP_Lab_(200, 200, 200)_logistic_identity : ΔE_max = 5.6715 , ΔE_mean = 0.7346 , ΔE_median = 0.3988
I find that the best tradeoff between complexity and performance is:
MLP_Lab_(50, 50)_logistic_identity : ΔE_max = 6.0237 , ΔE_mean = 0.9943 , ΔE_median = 0.6923
Training loss:
_logistic_identity_LOSS.png)
Prediction vs Real correlation:
_logistic_identity_CORR.png)
Again L seems to contain more errors than colour (a,b). I still didn't check which patches worked best and worse.
Delta E distribution:
_logistic_identity_HIST.png)
I also defined and checked some needed conversion functions:
- XYZ (D50) to Lab conversion
- Lab to XYZ (D50) conversion
- XYZ (D50) to sRGB (D65) conversion
- XYZ (D50) to ProPhoto RGB (D50) conversion
- Delta E calculation
I did a complete prediction with the NN over the input RAW values, and compared it to the expected theoretical values (right half rectangle on each patch). Obviously something went wrong because large errors are clearly visibe. I need to check where is the fault.

Regards