Why is the right 16X times less noisy ?. Shooting with 16X more exposure (+4EV) gives sqrt(16) = 4X better SNR .. so I would expect to be equal with 16 standard shots averaged 
It is not that simple but luckily it can be estimated more accurately from the SNR curves:
- In the sensor "highlights" where photon noise prevails, SNR increases by 3dB/EV (i.e. SNR is multiplied by sqrt(2) with each extra stop of exposure as you mention) but...
- In the sensor "deep shadows" where read noise prevails, SNR increases by 6dB/EV (i.e. SNR is multiplied by 2 with each extra stop of exposure).
For the case of HDR we are closer to the second situation since we are reallocating the deep shadows of the scene from the sensor's "deep shadows" (many stops below sensor saturation in the least exposed shot that preserves the highlights) to areas 4 stops closer to sensor saturation. That is why I made the 16x times less noise approximation.
But the real resulting SNR improvement will depend on the region we fall into. In my example this is the EV distribution of the +4EV crop:
(RAW histogram in EV)
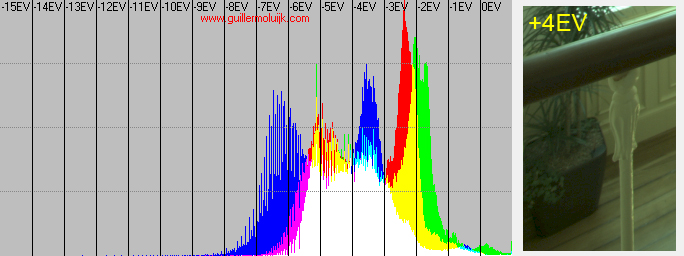
On average we can assume that the information from the crop is located around 5 stops below sensor saturation, this means in the 0EV shot the same information is on average located 9 stops below sensor saturation. Let's find out the exact SNR improvement from -9 to -5 following the SNR curves of the camera used (DxOMark info):
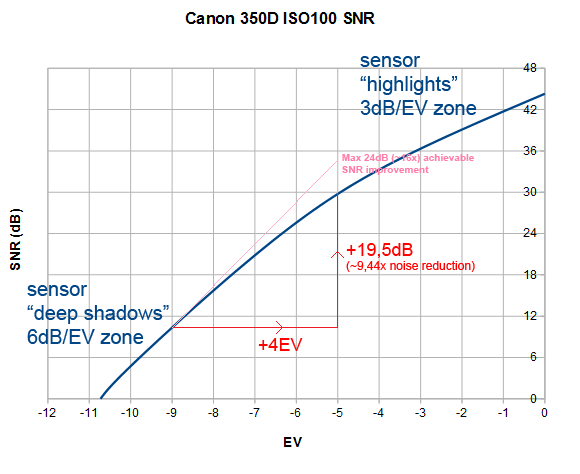
SNR improvement is around 19,5dB (less than 24dB but more than 12dB), i.e. noise was reduced by
9,44x (less than 16x but more than 4x).
To achieve the same improvement with averaging we would need: 9,44^2=89 standard shots (less than 256 but more than 16).
Since a real world scene is a continuous luminance distribution (my crop spreaded over around 6 stops of DR), the deepest shadows of the scene will always enjoy a larger SNR improvement than the
not so deep shadows. This is good news since it means more benefit is obtained where more help is initially needed to produce a well balanced output image in terms of SNR.
Regards